Ишемическое поражение головного мозга представляет собой одну из наиболее распространенных патологий и занимает лидирующее место среди инвалидизирующих заболеваний[3, 4]. Ухудшение кровоснабжения нервной ткани обусловливает достаточно быстрое уменьшение в клетках концентраций кислорода, глюкозы и других важнейших метаболитов, что создает условия для начала протекания патобиохимических процессов и формирует основу для запуска ишемического каскада[7]. В дальнейшем образование ишемического очага в существенной степени зависит от длительности и глубины трофических нарушений[5].
Палитра последующих метаболических изменений многообразна, но первопричиной формирования очага является полное или частичное прекращение тока крови в отдельной области. Примечательно, что механистическая причина нарушения мозгового кровообращения позволяет относительно просто смоделировать нарушение трофического состояния нервной ткани. Для достижения данной цели достаточно рассмотреть окклюзию отдельной ветви сосуда и, как следствие, снижение концентрации метаболитов в некоторой локальной области. При этом ее величина может характеризовать тип последующего ишемического инсульта.
На основе диффузионных и перфузионных характеристик головного мозга выделяют атеротромботический, кардиоэмболический и лакунарный типы ишемического инсульта[1, 8]. Следует отметить, что при малом размере поражения (до 1,0 мм) лакунарные повреждения не удается обнаружить даже с помощью современных средств клинической диагностики и это, безусловно, затрудняет эффективное проведение терапии[2]. Необходимо подчеркнуть, что во многих случаях нарушения мозгового кровообращения могут быть кратковременными и обратимыми, поэтому поддержание физиологических концентраций кислорода и метаболитов в области возможного ишемического очага является важнейшей компенсаторной функцией нервной ткани, позволяющей предотвратить развитие тяжелой патологии[15, 16].
Обобщенный теоретический анализ состояния сосудистой системы головного мозга является весьма сложной задачей по причине ее существенной вариабельности. В сочетании с тонкой гетерогенной структурой мозга вопрос о формулировке закономерностей возникновения трофических нарушений для конкретных областей с последующим формированием ишемического очага представляется неразрешимым. В то же время особое значение имеет применение методов компьютерного моделирования для описания конкретных паттернов.
Цель исследования: сравнительный анализ влияния геометрии единичного разветвления кровеносного сосуда на формирование ишемического очага.
МАТЕРИАЛЫ И МЕТОДЫ
Моделирование пространственно-временного распределения концентрации метаболита проводилось в локальной области, включавшей в себя один сосуд с одной точкой ветвления (рис. 1), из которого происходила диффузия метаболитов в ткань. Без ограничения общности рассуждений калибр материнской ветви R принимался равным 60 мкм. Хорошо известно, что геометрическое разветвление кровеносных сосудов происходит не случайным образом — оно подчиняется весьма строгим закономерностям, обусловленным гидродинамикой течения крови и свойствами сосудистой стенки[17, 18]. Более того, не только геометрия бифуркации, но и калибр дочерних ветвей и их длина определяются соотношениями, полученными в рамках представлений о минимальности совершаемой работы и минимуме общего сопротивления системы потоку[10, 11]. Совокупность вышеупомянутых предположений можно условно обозначить как теорию оптимального ветвления (бифуркации)[13, 14].
Рис. 1. Схематическое изображение сосуда с одной точкой ветвления.
Примечание. Различные варианты бифуркации можно условно объединить в две группы ― симметричные (А) и асимметричные (Б). В случае симметричных точек ветвления α1 ≈ α2
и r1 ≈ r2. При асимметричном ветвлении не только существенно меняется угол отклонения от оси материнской ветви: α1
<< α2, — но и происходит изменение калибра дочерних ветвей: r1
> r2; r1 ~ R. Локальная область, заключенная между ветвями сосуда и расположенная на биссектрисе ветвления на расстоянии d0
от точки бифуркации, представляет собой центр предполагаемой ишемической области (IA)
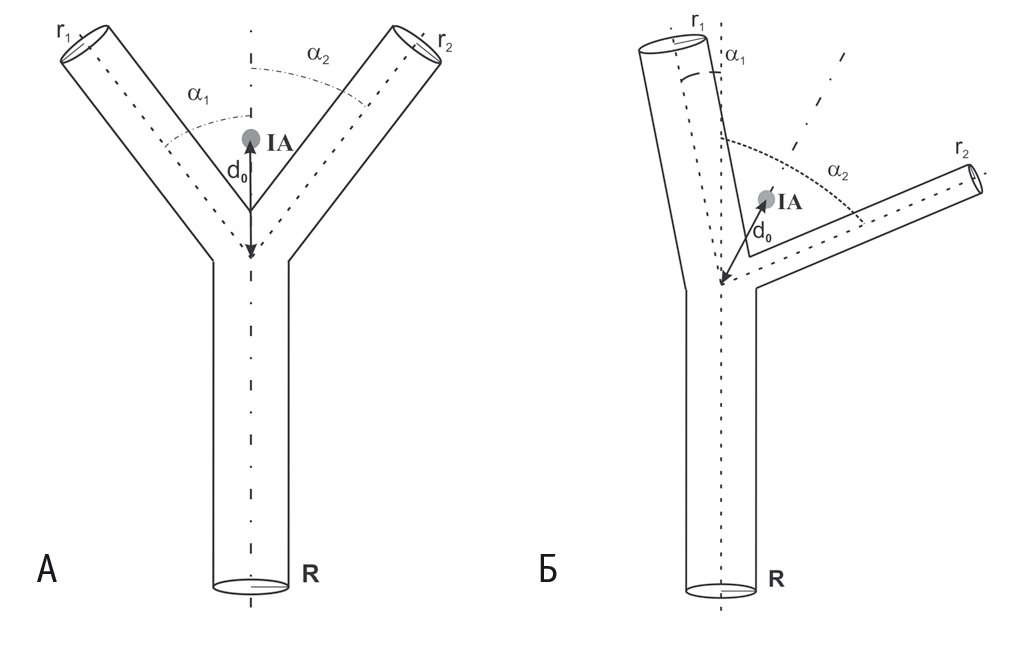
Таким образом, хотя форма сосудистого дерева разнообразна, каждый отдельный локальный участок достаточно жестко детерминирован. Следует обратить внимание, что среди всех случаев можно выделить две группы точек ветвления. В одном случае дочерние ветви расходятся от точки бифуркации симметрично оси материнской ветви (см. рис. 1А), а в другом — несимметрично (см. рис. 1Б), т. е. биссектриса угла ветвления существенно отклоняется от оси материнской ветви. Совершенно очевидно, что между двумя ветвями образуется область, трофическое обеспечение которой будет осуществляться исключительно путем диффузии метаболитов от их стенок. Она должна располагаться вблизи точки бифуркации и равноудаленно от поверхности ветвей. Область ишемии (ischemic area — IA) представлена на рисунке 1.
Фантом выбранного участка нервной ткани строился на основании принципов, изложенных ранее[6, 20]. В качестве областей источников метаболитов были приняты полости кровеносных сосудов[20]. Пространственно-временные распределения метаболитов были рассчитаны на основании аналитических решений первой краевой задачи для сферически-симметричного источника[6]. Формирование трофических нарушений в предполагаемой ишемической области рассматривалось как следствие окклюзии дочерней ветви сосуда и моделировалось путем исключения из совокупности источников этой ветви. Полученные объемные пространственно-временные градиенты концентрации глюкозы были представлены в виде послойных имиджей.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Пространственно-временные градиенты концентрации глюкозы вблизи отдельного сосуда с одной точкой ветвления показаны на рисунке 2. Видно, что симметричная и асимметричная системы при отсутствии окклюзии имеют сходные градиенты концентрации глюкозы. Различие в области IA для рассматриваемых фантомов составило 15% и было обусловлено особенностями геометрии.
Рис. 2. Пространственные распределения концентрации глюкозы вблизи сосуда с симметричной (А) и асимметричной (Б) точкой ветвления, а также соответствующие изменения градиентов при окклюзии ветви (В, Г).
Примечание. Параметры моделирования принимали следующие значения: концентрация глюкозы в кровотоке ― 5 мМ; коэффициент диффузии D = 300 мкм2с–1[19]; коэффициент поглощения глюкозы средой k = 0,3 с–1. Полость сосуда выделена и заштрихована. Дочерняя ветвь, подвергшаяся окклюзии, обозначена двойной штриховкой

Однако при моделировании окклюзии относительное изменение содержания глюкозы в точке наблюдения существенным образом зависело от исходной геометрии бифуркации. Так, в случае симметричного ветвления падение уровня глюкозы от значения, наблюдавшегося до окклюзии, составило 41%, а при асимметричной бифуркации — лишь 22%. Столь существенные различия указывают на то, что формирование области снижения трофики после окклюзии малого кровеносного сосуда в значительной степени зависит не только от уровня метаболизма нервной ткани, но и от взаимного расположения функционирующих ветвей.
Наше наблюдение относительно значения геометрии бифуркации кровеносных сосудов находит подтверждение и в работах по изучению других тканей. Так, в случае диабетической ретинопатии экспериментально показано, что степень увеличения угла бифуркации малого кровеносного сосуда может рассматриваться как маркер тяжести и прогноза заболевания[12]. В то же время N. Chapman и соавт. продемонстрировали, что увеличение угла бифуркации сосуда наблюдается в ответ на понижение насыщения крови кислородом[9]. Данное обстоятельство косвенным образом экспериментально подтверждает обнаруженное нами значение асимметричных структур ветвления сосудов для поддержания трофического уровня нервной ткани при окклюзии отдельных ветвей. Необходимо также отметить, что полученный в нашей работе результат носит общий характер и может быть качественно экстраполирован на множество метаболитов, диффундирующих вблизи стенки сосудов.
ЗАКЛЮЧЕНИЕ
Таким образом, на основании проведенного в работе теоретического анализа определено, что трофическое снабжение локальной области, потенциально являющейся зоной формирования ишемического очага, в значительной степени зависит от геометрии ветвления сосудистой системы.








